Entenda a classificação dos sistemas produtivos

É impossível dar uma visão unificada da programação da produção, prescindindo do tipo de sistema produtivo.

Por is­so, é necessário classificá-los de acordo com algumas características-tipo.

Obtém-se uma classificação útil distinguindo três dimensões: variedade de produtos, variedade de processo e tipo de demanda.

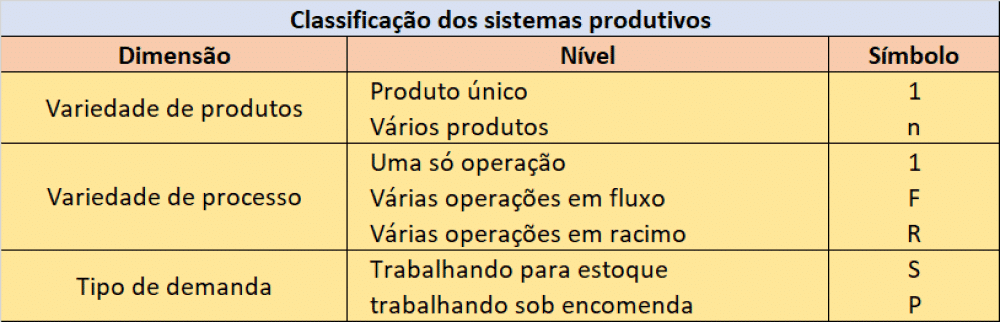
Por sua vez, a cada dimensão podem ser atribuídos vários níveis, como mostra o qua­dro “Classificação dos sistemas produtivos”.

Para efeito de análise, cada sistema produtivo será designado mediante a sequência dos símbolos de suas dimensões, separados por barras.

Assim, por exem­plo, 1/1/S significa um sistema de um só produto, com uma só operação e trabalhando para estoque, etc.

Breve análise dos diferentes tipos de sistemas

• Sistema 1/1/S.

O principal problema desse tipo de sistema aparece quando a produção é intermitente, sendo preciso decidir quanto se deve produzir em cada lançamento.

Aqui, a análise se limita ao caso da figura “Demanda regular a uma velocidade constante e conhecida”, que representa a evolução dos estoques com uma demanda regular de D unidades por período e uma taxa de produção de p unidades por período (por exemplo, D = 10.000 unidades/mês e p = 30.000 unidades/mês).

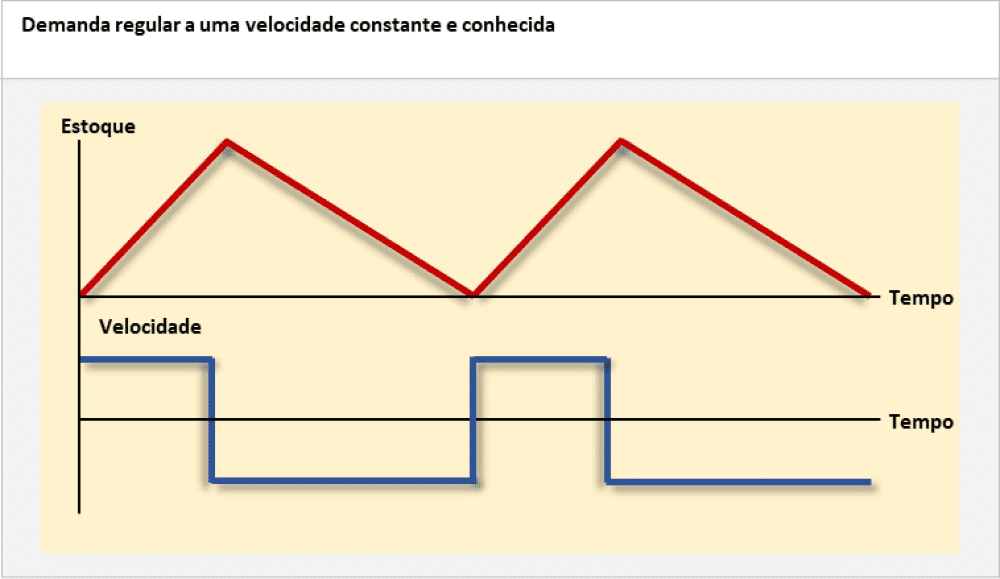
_{Nestes dois gráficos, o sistema 1/1/S de produção intermitente. A figura apresenta a evolução dos estoques de uma demanda regular de D unidades por período e uma taxa de produção de p unidades por período. Na mesma figura, aparece o gráfico das velocidades de entrada e saída do estoque igual a (p – D), enquanto se está produzindo (e vendendo), e igual a – D (diminuição do estoque) enquanto se vende sem produzir.}

Na mesma figura, apresenta-se o gráfico das velocidades de entrada e saída do estoque, tal que p – D enquanto se está produzindo (e vendendo) e – D (diminuição do estoque) enquanto se ven­de sem produzir.

Chamando-se K ao custo de lançamento e c ao de posse por uni­dade e ano, pode-se provar que os lotes ótimos devem ser calculados segundo a fórmula:

Q = [[[ ]]] [[[ ]]]

Essa expressão é conhecida como fórmula do lote econômico de produção e é parecida com a do lote econômico de compra, com exceção do fator (1 – D / p) do denominador.

• Sistema 1/n/S.

É conveniente distinguir dois subsistemas, dependendo se a produção é contínua ou é intermitente.

O primeiro, 1/n/S com fabricação contínua, inclui um processo de grande eficiência produtiva e de uso comum: a linha de montagem.

Esse processo é a síntese da filosofia da divisão do trabalho.

Sua base foi estabelecida pelo próprio Adam Smith, mas só foi levada à prática industrial de grande volume por Henry Ford.

O produto que se quer fabricar é ana­lisado até decompô-lo em atividades elementares.

Por exemplo: suponhamos que se trata de montar um produto simples, como uma esferográfica; a produção diá­ria exigida é de 10.000 unidades e o tem­po total de montagem de uma unidade é de um minuto; assim, pois, serão necessários diariamente 10.000 minutos.

Portanto, pode-se conseguir esta produção em 10.000 / 480 = 20,8 operários ou, arredondando, com 21 operários.

De acordo com a filosofia da linha de montagem, a montagem da esferográfica deve ser subdividida em várias tarefas (montagem do tubo, aparafusado no corpo, etc), atribuindo-se a cada operário algumas operações, partindo da premissa de que a especialização cria eficiência.

Além disso, podem-se eliminar os estoques intermediários sincronizando as diferentes atividades: quando um operário termina as tarefas que lhe foram atribuídas, a peça em curso passa ao operário seguinte, que por sua vez acabou suas tarefas na peça anterior.

Portanto, a operação eficiente de uma linha de montagem requer: uma adequada divisão de trabalho em atividades elementares; uma especialização dos operários em atividades; uma disposição especial do local de trabalho de cada operário, com as ferramentas e os utensílios que facilitem sua tarefa; uma adequada repartição das tarefas entre os componentes da linha para conseguir o sincronis­mo desejado.

O esforço para fazer deslanchar uma linha de montagem pode ser considerável, já que os estudos exigidos pela divisão do trabalho, pela especialização e pela disposição do local do trabalho de cada operário podem consumir muito tempo.

Além disto, quando uma linha foi preparada para determinada velocidade de produção, a repartição de tarefas entre os componentes da linha faz com que mudá-lo seja caro e lento.

Por isso, as linhas de montagem são utilizadas fundamentalmente para produtos maduros, nos quais a eficiência e o baixo custo se consideram características muito essenciais.

A grandeza mais importante de uma linha de montagem é o seu tempo de ciclo: o tempo que transcorre entre duas saídas sucessivas de uma unidade do produto da linha de montagem.

Em uma linha sequencial, onde cada tarefa é realizada em uma só estação, este é o tempo disponível para realizar o trabalho de cada estação.

O cálculo de uma linha se divide em duas partes: determinação dos parâmetros básicos e definição de tarefas para as estações.

O dado primário costuma ser a produção desejada por unidade de tempo.

Em nosso exemplo, propôs-se uma produção de 4 unidades por hora.

O tempo de ciclo é de 15 minutos (60 / 4).

Daí se pode determinar facilmente o número mínimo necessário de estações, levando em conta que cada estação contribui com um tempo de ciclo.

Se o conteúdo em trabalho do produto é de 75 minutos, com um tempo de ciclo 15 o número de estações é 75 / 15 = 5.

Mas se o tempo de ciclo é de 10 são necessárias 8 estações, como resultado de arredondar 75 / 10 = 7,5.

Uma vez determinados os parâmetros básicos da linha, é preciso atribuir as tarefas às estações para ter o mínimo tempo ocioso total.

Este problema é mais complicado.

Até há poucos anos, a única técnica era a da experimentação.

Re­centemente, elaboraram-se métodos aproximados que podem ser processados em microcomputadores e que conseguem equilibrar satisfatoriamente linhas complicadas.

Na análise do subsistema 1/F/S intermitente, para simplificar, se partirá do ca­so de dois centros e se considerará apenas o caso da demanda uniforme.

A figura “Evolução dos estoques depois de sua passagem pelos centros de traba­lho” mostra essa evolução em função da demanda final D e a partir do lote do cen­tro 1 e do lote do centro 2.

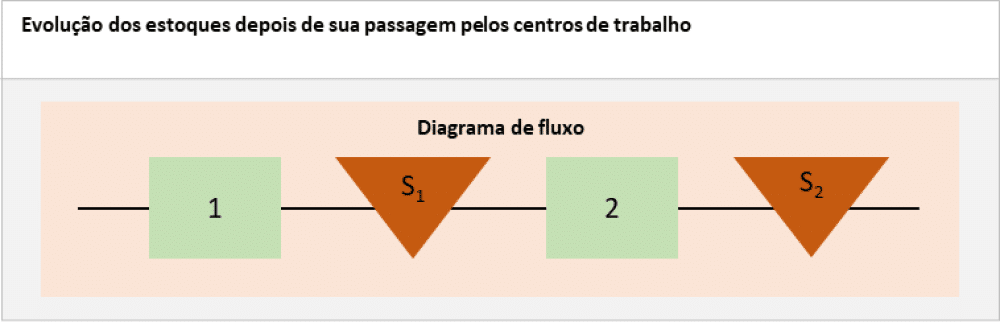
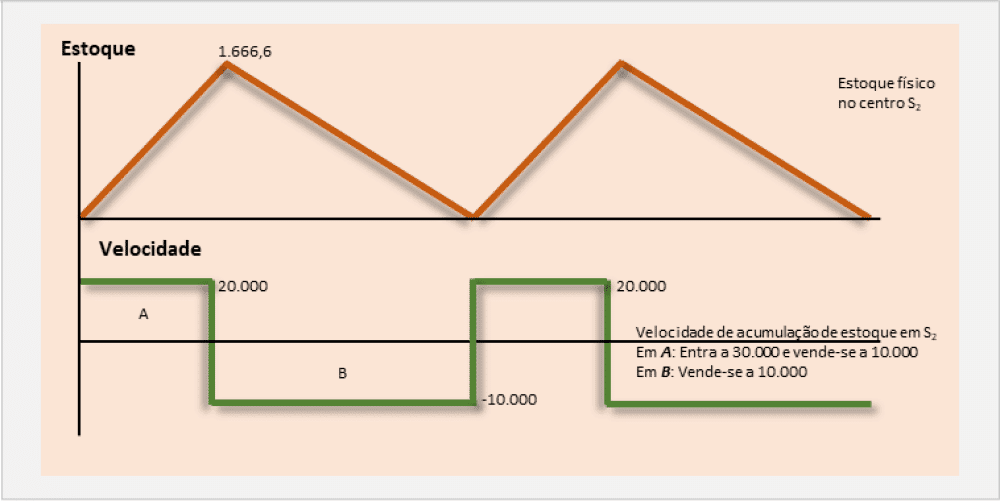
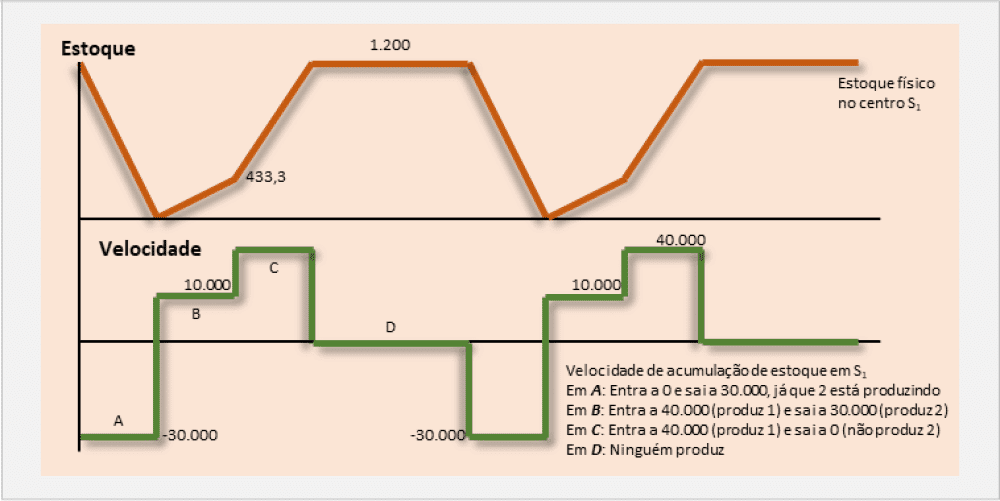
_{A figura mostra a evolução dos estoques em função da demanda final D e a partir dos lotes de dois centros de trabalho (1 e 2) para ilustrar o sistema 1/F/S intermitente. A mesma indica a velocidade na qual se realiza o preenchimento de cada estoque. A curva do estoque de acabado (S2) é em dente de serra, mas a do estoque depois de SI é complicada, já que a velocidade de acumulação do produto depende do estado da produção em ambos os centros. É isso que dificulta a determinação de bons lotes em um sistema em várias etapas.}

Na mesma figura, indica-se a velocidade de preenchimento de cada estoque.

Observa-se que o gráfico do estoque acabado (depois de 2) é em dente de serra, mas o do estoque depois de 1 é muito complicado, já que a velocidade de acumulação do produto depende do estado de produção de am­bos os centros.

Esta característica tornaria muito difícil a determinação aproximada de bons lotes em um sistema em vá­rias etapas.

Introduzindo-se o importan­te conceito do estoque de escalão, o problema pode ser resolvido de forma satisfatória.

O estoque de escalão em um centro, como o 1, compreende todo o produto que passou pelo centro e que ainda não foi vendido.

Na figura “Estoque de escalão”, indicam-se os gráficos deste, correspondentes ao exemplo da figura “Evolução dos estoques depois de sua passagem pelos centros de trabalho”.

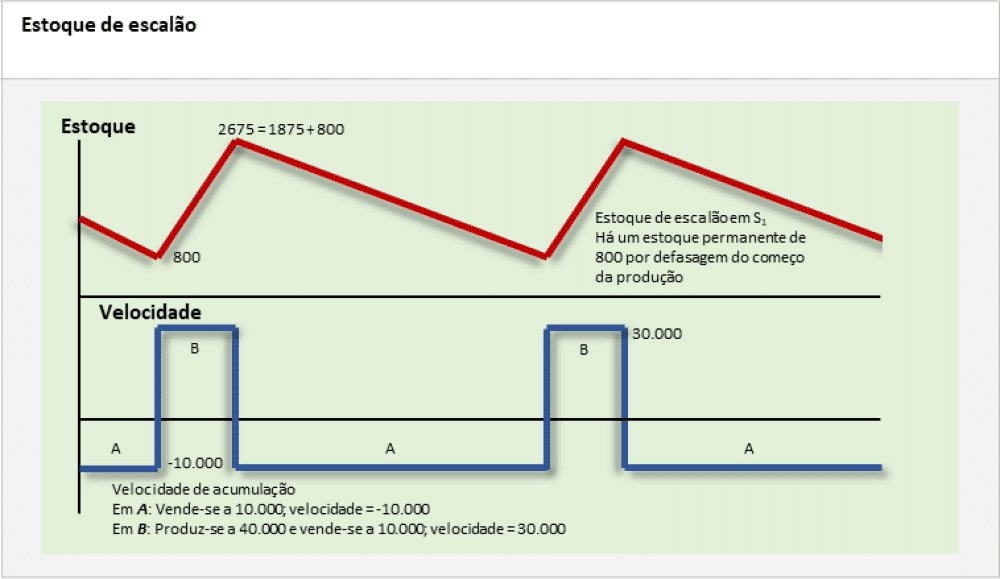
_{A figura Estoque de escalão inclui os gráficos deste tipo de estoque correspondentes à figura anterior. Este conceito permite resolver de forma satisfatória o problema da dificuldade da determinação de bons lotes em um sistema de várias etapas. O estoque de escalão em 1 compreende todo o produto que passou pelo centro. Como o estoque de escalão cresce na velocidade da produção e diminui na velocidade das vendas, em qualquer nível há sempre um gráfico em dente de serra e seu valor médio é fácil de ser calculado. Omitiu-se o gráfico correspondente ao estoque de escalão em 2, já que é idêntico ao do estoque normal neste depósito.}

Já que o estoque de escalão cresce na velocidade da produção do cen­tro e diminui na velocidade das vendas, o estoque de escalão em qualquer nível tem sempre um gráfico em forma de den­te de serra e, por conseguinte, seu valor médio é facilmente calculável.

Disso é possível deduzir as duas regras seguintes da programação:

“Cada vez que se produz em 1, também se deve produzir em 2”; “O lote de produção de 1 é um múltiplo exato do lote de produção de 2”.

As regras descritas acima podem ser aplicadas como guia para os sistemas com mais escalões.

• Sistema n/l/S.

Este sistema apresenta-se quando há uma única máquina, que atua como gargalo e pela qual deve pas­sar toda a produção.

Frequentemente, a máquina só pode processar um produto cada vez.

Casos típicos na prática são os túneis de pintura e os fornos contínuos.

O programa de produção prepara-se normalmente estabelecendo-se a frequência da produção de cada artigo em cada ciclo.

Dadas as frequências, ordená-las em uma sequência adequada de acordo com os custos de mudança.

Dada a sequência, calcular o lote de cada produto a ser fabricado, segundo o que foi combinado.

• Sistemas n/F/S e n/R/S.

A maior parte dos sistemas têm os n produtos orga­nizados em níveis, isto é, alguns utilizam os outros como componentes.

Por isso o problema de decidir consiste em determi­nar um programa de produção para os diferentes produtos: que satisfaça a deman­da independente dada pelas vendas; que esteja em condições de fornecer os componentes no momento de começar a pro­dução de um artigo pai que tiver necessidade deles; que tenha custos aceitáveis e possa ser realizado dentro das limitações das capacidades de produção fixadas pe­lo plano de produção global.

Entre os enfoques práticos para solucionar o problema, sobressai o chamado enfoque MRP, que se desdobra da seguinte maneira.

Define-se um programa-mestre de produção, que abarca essencialmente os produtos acabados e que será tomado como base de toda a programação dos produtos com demanda depen­dente.

Definem-se regras de cálculo de lo­tes para os artigos não incluídos no plano-mestre de produção, que serão aplicadas automaticamente pelo computador.

A partir das composições e das rotas, determinam-se as quantidades que se de­ve produzir de cada artigo dependente e as cargas dos centros.

Não se faz um esforço para encaixar a produção dentro das capacidades, embora às vezes haja tentativas de suavização ou de carga fi­nita baseadas em alguma aproximação.

Como se pode verificar, um sistema MRP baseado no computador é um verdadeiro sistema de informação, às vezes de grande complexidade.

Existem paco­tes de programas comerciais, normalmente a um preço elevado, que permitem tra­tar dezenas de milhares de referências.

Com o aparecimento dos microcomputadores, estão surgindo no mercado paco­tes MRP que se encontram ao alcance tanto da pequena como da média empresa.

Sistemas trabalhando sob encomenda

As principais características diferenciais da modalidade de trabalho sob encomenda são:

• A grande variedade de produtos, e por isso, com frequência, cada pedido costu­ma ser considerado um produto;
• O aparecimento das datas entrega, que se aplicam aos pedidos individuais e que são um compromisso de produção que substitui o de servir a demanda;
• A frequente manutenção da identidade do pedido ao longo da produção;
• A grande dificuldade para a realização de previsões, pelo menos em alguns produtos.

Estas características contribuem para tornar mais difícil a programação de sistemas sob encomenda.

• Sistema n/l/P.

O problema central deste sistema é o cumprimento das datas de entrega com eficiência.

Costuma-se distinguir dois casos: sistemas de carga planejada e sistemas de serviço.

Nos primeiros, é normal utilizar regras de prioridade para decidir a sequência das operações.

Uma regra que funciona bem é a da folga média residual, que ordena os pedidos em sentido crescente do índice:

Data entrega – Data de hoje / Tempo de processo do pedido

Por exemplo, se temos seis pedidos com datas de entrega nos dias 10, 15, 12, 14, 18 e 20, a partir de uma origem arbitrária e de tempos de processos de 1, 2, 1, 4, 5 e 2 dias, respectivamente, supondo que o dia em curso é o 9, então o método dá lugar à sequência de processo 1, 4, 5, 2, 3, 6.

Quanto aos sistemas de serviço – uma clínica, uma oficina mecânica, um restaurante, são exemplos típicos, há uma grande variabilidade dos tempos de processo e uma possível irregularidade das demandas, que chegam quase ao acaso.

Neste caso produz-se um fenômeno de interferências, também chamado fenômeno de caudas.

Devido à irregularidade da carga de chegada e à dos tempos de serviço, o centro pode ficar temporariamente sem trabalho, apesar de ter uma elevada carga média.

Por isso, a regra fundamental para esses sistemas é a impossibilidade de conseguir simultaneamente uma elevada utilização do centro produtivo e um adequado prazo de entrega.

O aumento de uma prejudica o outro, e vice-versa.

Nos sistemas de serviço, é indispensável prever uma taxa da utilização do centro bastante inferior à unidade, caso se quer dar bom serviço.

Na prática, interessa aumentar a utilização do centro sem prejudicar o serviço.

Isto só pode ser conseguido de duas formas: ou introduzindo trabalhos que podem ser interrompidos, isto é, atribuindo ao centro trabalhos que possa realizar quando estiver livre, mas que podem ser deixados quando chegar um pedido a processar; ou tratando de reduzir ao mínimo as interferências motivadas pela variabilidade das entradas e do tempo de processo.

Uma clínica pode, por exemplo, programar as operações de maneira muito detalhada para aumentar a disponibilidade das salas de cirurgia, e depois verificar que a variabilidade do tempo de processo, de operação, cria por si só interferências notáveis e pode deixar sem efeito o sistema mais elaborado de previsão e de programação.

• Sistema n/F/P.

Este sistema pode ser tratado como uma sequência de sistemas n/l/P, embora tenha o inconveniente de ser muito mais complexo.

• Sistema n/R/P.

Embora neste caso se­ja possível distinguir os dois tipos de situações, planejada e de serviço, a sequência operativa destes sistemas assemelha-se muito mais ao segundo tipo do que ao primeiro.

A este tipo pertence o JobShop, ou oficina mecânica, protótipo de muitos sistemas com estrutura funcional, isto é, organizados por centros de proces­so e que admitem qualquer produto que neles se possa processar.

Destas considerações pode-se deduzir que a regra básica do funcionamento des­tes sistemas é a enunciada para n/l/P:

“Não é possível conseguir ao mesmo tempo uma boa utilização e um prazo de entrega curto”.

Portanto, a programação de tais sistemas não pode basear-se na diminuição da sua variabilidade.

Por essa razão, a maioria dos enfoques que pretendem manter em dia um programa de produção – por exemplo, por meio de um diagrama de Gantt de atividades ou de máquinas – estão condenados ao fracas­so e levam seus responsáveis ao desespe­ro.

Primeiro, pela complexidade que su­põe criar um programa; segundo (e mui­to mais importante), pela grande variabilidade do sistema, derivada da interferência entre os produtos, as rotas e os centros.

Leia mais em:

• Entenda o conceito de sistema de controle de produção
• Como entender o planejamento e programação da produção
• Entenda o planejamento da produção

_{Fonte: Josep Riverola García – Doutor engenheiro de indústrias têxteis, master of Sciences in Operations Research, Ph.D.in Operations Research e catedrático da Universidade Politécnica de Barcelona.}